LeetCode: Graphs II 01 BFS
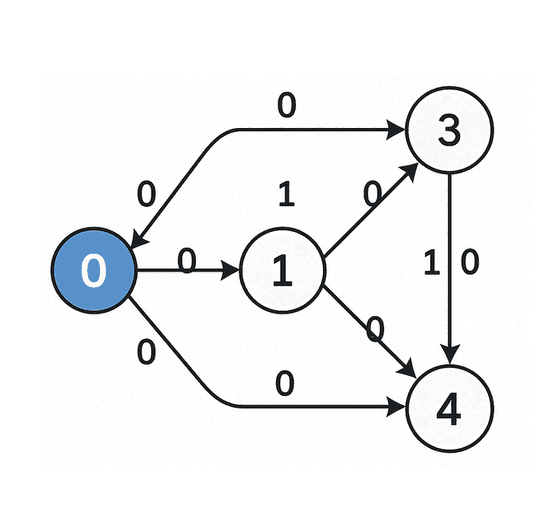
Table Of Contents
Zero One BFS Algorithm Intro
Graph Requirements
Output
Video Animation
Pseudo Code
Time Complexity
Space Complexity
IRL Use Case
What is Zero One BFS Algorithm
1006. Network Delay Time ::1:: - Medium
Topics: Depth First Search, Breadth First Search, Graph, Heap (Priority Queue), Shortest Path
Intro
You are given a network of n nodes, labeled from 1 to n. You are also given times, a list of travel times as directed edges times[i] = (ui, vi, wi), where ui is the source node, vi is the target node, and wi is the time it takes for a signal to travel from source to target. We will send a signal from a given node k. Return the minimum time it takes for all the n nodes to receive the signal. If it is impossible for all the n nodes to receive the signal, return -1.
| Example Input | Output |
|---|---|
| times = [[2,1,1],[2,3,1],[3,4,1]], n = 4, k = 2 | 2 |
| times = [[1,2,1]], n = 2, k = 1 | 1 |
| times = [[1,2,1]], n = 2, k = 2 | -1 |
Constraints:
1 ≤ k ≤ n ≤ 100
1 ≤ times.length ≤ 6000
times[i].length == 3
1 ≤ ui, vi ≤ n
ui != vi
0 ≤ wi ≤ 100
All the pairs (ui, vi) are unique. (i.e., no multiple edges.)
Abstraction
Given a graph, each node with 1 edges, determine how much time is needed to get from start node to target node.
Space & Time Complexity
| Solution | Time Complexity | Space Complexity | Time Remark | Space Remark |
|---|---|---|---|---|
| Bug | Error |
|---|---|
Brute Force:
| Aspect | Time Complexity | Space Complexity | Time Remarks | Space Remarks |
|---|---|---|---|---|
Find the Bug:
Solution 1: [Dijkstra's] BFS And MinHeap To Keep Shortest Path - Advanced Graphs/Advanced Graphs
def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:
# Dijkstra's Algorithm (Single-Source Shortest Path):
# We want the minimum time for a signal sent from node k
# to reach all n nodes in a directed graph with non-negative weights.
# Key Ideas:
# 1. Model the network as a directed weighted graph.
# 2. Use a min-heap to always expand the node with the smallest
# known signal arrival time.
# 3. Maintain a dictionary of shortest known times to each node.
# 4. If all nodes are reached, return the maximum of these times.
# 5. If some node is unreachable, return -1.
# Build adjacency list: graph[src] = [(dest, weight), ...]
# tc: O(edge)
graph = defaultdict(list)
for u, v, w in times:
graph[u].append((v, w))
# Min-Heap:
# Each entry is (time_to_reach_node, node)
# sc: O(node)
heap = [(0, k)]
# Dictionary to track shortest known time to each node
# Invariant: once a node is added here, its shortest time is finalized
shortest_time = {}
# tc: each node/edge O(e) processed via O(log n) heap operations O(e log n)
while heap:
# Pop node with smallest known arrival time
time, node = heapq.heappop(heap)
# Skip if this node already has a finalized shortest time
# (We found a better path earlier)
if node in shortest_time:
continue
# Record shortest time to reach this node
shortest_time[node] = time
# Explore Choices:
# Relax all outgoing edges from this node
for neighbor, wt in graph[node]:
# If neighbor not finalized, push updated time candidate
if neighbor not in shortest_time:
heapq.heappush(heap, (time + wt, neighbor))
# After processing:
# If not all nodes were reached, signal cannot reach everyone
if len(shortest_time) != n:
return -1
# Result:
# The total network delay is the maximum shortest arrival time
res = max(shortest_time.values())
# overall: tc O(e log n)
# overall: sc O(n + e)
return res