LeetCode: Graphs II Dijkstras BellmanFord Single Source Shortest Path
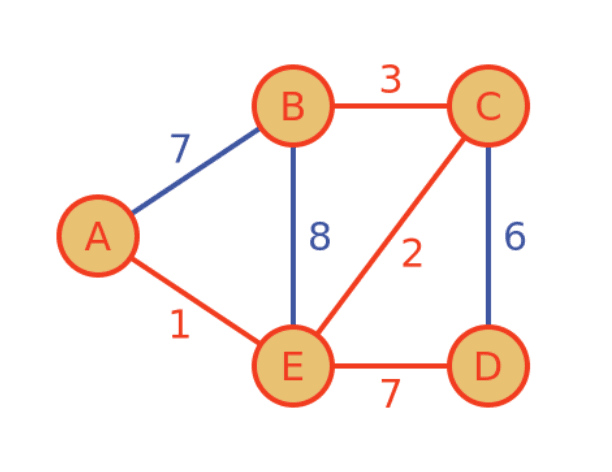
Dijkstra's Algorithm Intro
Intro
Dijkstra's Algorithm is a graph traversal algorithm used to find the shortest path from one source node to all other nodes in weight graph with non-negative edge weights.
It is often described as a Greedy BFS using a MinHeap/Priority Queue.
Like BFS, it expands outward from the source node. Unlike BFS, it chooses the next closest node by total distance, not by layer
Graph Requirements
- Weighted Graph
- Non-negative Edge Weights
- Directed or Non Directed
- Represented Using:
- Adjacency List
- Adjacency Matrix
Output
A shortest path tree rooted at the source. Any node not visited is unreachable.
Video Animation
https://www.youtube.com/watch?v=_lHSawdgXpI
Greedy BFS Analogy
Always expand the node with the smallest currently known distance
Pseudo Code
def dijkstra(graph, source):
# 1. Initialize all distances to ∞
# 2. Set source distance = 0
# 3. Use MinHeap to always expand smallest distance node
# 4. Relax edges (update neighbors if shorter path found)
# 5. Continue until all nodes processed
# Initialize distances
distances = {node: float('inf') for node in graph}
distances[source] = 0
# MinHeap (priority queue)
min_heap = []
# Push all distances to minHeap
heapq.heappush(min_heap, (0, source)) # (distance, node)
# Tracking closed nodes
visited = set()
# Process nodes
while min_heap:
# Smallest distance node
current_dist, node = heapq.heappop(min_heap)
# Skip if already finalized
if node in visited:
continue
# Close Node
visited.add(node)
# Relax edges
for neighbor, weight in graph[node]:
new_dist = current_dist + weight
if new_dist < distances[neighbor]:
distances[neighbor] = new_dist
heapq.heappush(min_heap, (new_dist, neighbor))
# Map of shortest path from source node to all nodes
return distancesTime Complexity
V = number of vertices E = number of edges
Using adjacency list + minHeap: O((V + E) log v)
Each vertex is inserted into the minHeap at most once. Each edge may cause a minHeap update. Heap operations cost log V
Space Complexity
V = number of vertices E = number of edges
Using adjacency list + minHeap: O(V)
Distance Map: O(V) Visited Set: O(V) MinHeap: O(V)
IRL Use Case
-
GPS Navigation Systems Finding the shortest driving route between locations
-
Network Routing Determining the least-cost path for packet transmission
-
Game AI Path Finding NPC movement optimization on weighted maps
Bellman Ford Algorithm Intro
Intro
Bellman Ford is a single source shortest path algorithm that works for graphs with negative edge weights.
It finds the shortest distance from a source node to all other nodes in a weighted graph and can detect negative weight cycles.
Unlike Dijkstra, it does not require non-negative weights, but it is slower
Graph Requirements
- Weight Graph, can include negative weights
- Directed or Undirected
- No requirements for non-negative edges
- Represented Using:
- Adjacency List
- Edge List
Output
- Shortest distance from a source to every other node
- Can indicate if a negative weight cycle exists (impossible to define shortest paths)
Video Animation
https://www.youtube.com/watch?v=obWXjtg0L64
Relaxing Analogy
Think of it as repeatedly 'relaxing' edges: For each
Pseudo Code
def bellman_ford(edges, V, source):
# Initialize distances
dist = [float('inf')] * V
dist[source] = 0
# Relax all edges V-1 times
for _ in range(V - 1):
for u, v, w in edges:
if dist[u] + w < dist[v]:
dist[v] = dist[u] + w
# Check for negative weight cycles
for u, v, w in edges:
if dist[u] + w < dist[v]:
raise ValueError("Graph contains a negative weight cycle")
return distTime Complexity
V = number of vertices E = number of edges
Relaxing All Edges V-1 Times: O(V * E)
Space Complexity
V = number of vertices E = number of edges
Distance Array: O(V)
IRL Use Case
-
Network Routing Supports networks where some paths may have penalties or negative costs
-
Timing Scheduling Problems Detect impossible schedules due ot negative constraints
743. Network Delay Time ::1:: - Medium
Topics: Depth First Search, Breadth First Search, Graph, Heap (Priority Queue), Shortest Path
Intro
You are given a network of n nodes, labeled from 1 to n. You are also given times, a list of travel times as directed edges times[i] = (ui, vi, wi), where ui is the source node, vi is the target node, and wi is the time it takes for a signal to travel from source to target. We will send a signal from a given node k. Return the minimum time it takes for all the n nodes to receive the signal. If it is impossible for all the n nodes to receive the signal, return -1.
| Example Input | Output |
|---|---|
| times = [[2,1,1],[2,3,1],[3,4,1]], n = 4, k = 2 | 2 |
| times = [[1,2,1]], n = 2, k = 1 | 1 |
| times = [[1,2,1]], n = 2, k = 2 | -1 |
Constraints:
1 ≤ k ≤ n ≤ 100
1 ≤ times.length ≤ 6000
times[i].length == 3
1 ≤ ui, vi ≤ n
ui != vi
0 ≤ wi ≤ 100
All the pairs (ui, vi) are unique. (i.e., no multiple edges.)
Abstraction
Given a graph, each node with 1 edges, determine how much time is needed to get from start node to target node.
Space & Time Complexity
| Solution | Time Complexity | Space Complexity | Time Remark | Space Remark |
|---|---|---|---|---|
| Bug | Error |
|---|---|
Brute Force:
| Aspect | Time Complexity | Space Complexity | Time Remarks | Space Remarks |
|---|---|---|---|---|
Find the Bug:
Solution 1: [Dijkstra's] BFS And MinHeap To Keep Shortest Path - Advanced Graphs/Advanced Graphs
def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:
# Dijkstra's Algorithm (Single-Source Shortest Path):
# Find minimum time for node k signal to reach all nodes in
# a directed weighted graph
# Similar to BFS layer expansion, bt instead of expanding level by level,
# we expand the node with the smallest current travel time using a minHeap
# Greedy:
# Once a node is popped from the hea, its shortest time is finalized
# because weights are non negative
# Graph Construction:
# Build Adjacency List:
# graph[u] = [(v, weight), ...]
# Key Ideas:
# 1. Model the network as a directed weighted graph.
# 2. Use a min-heap to always expand the node with the smallest
# known signal arrival time.
# 3. Maintain a dictionary of shortest known times to each node.
# 4. If all nodes are reached, return the maximum of these times.
# 5. If some node is unreachable, return -1.
# sc: O(E) adjacency list storage
graph = defaultdict(list)
# Build adjacency list: graph[src_node] = [(dest_node, weight), ...]
# tc: O(E) iterate over all edges
for u, v, w in times:
graph[u].append((v, w))
# Min-Heap:
# ensures we always explore the node with the smallest known travel time next
# sc: O(V) worst case
heap = [(0, k)]
# Invariant:
# Tracks finalized shortest time to each node
# Once a node enters shortest_time,
# its minimum distance is guaranteed final, because graph is non-negative
# sc: O(V)
shortest_time = {}
# Dijkstras Traversal (Greedy BFS)
# - each edge may be pushed into heap
# - heap operations cost log V
# tc: O(E log V)
while heap:
# MinHeap root holds node with smallest known arrival time
# tc: O(log V)
time, node = heapq.heappop(heap)
# Skip outdated candidates:
# another shorter path already finalized this node
# tc: O(1)
if node in shortest_time:
continue
# Finalize shortest time
shortest_time[node] = time
# Explore Choices (edge relaxation):
# Try extending path to neighbors
for neighbor, wt in graph[node]:
# Only explore neighbors if time not yet finalized
if neighbor not in shortest_time:
# push time to minHeap
# tc: heap push
heapq.heappush(heap, (time + wt, neighbor))
# Final Validation:
# if not all nodes were reached, signal cannot propagate everywhere
# tc: O(1)
if len(shortest_time) != n:
return -1
# Network delay = longest shortest path
# (last node to receive signal)
# tc: O(V)
res = max(shortest_time.values())
# overall: tc O(E log V)
# overall: sc O(V + E)
return resSolution 2: [Bellman Ford] BFS And MinHeap To Keep Shortest Path - Advanced Graphs/Advanced Graphs
def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:
# Bellman For Algorithm (Single-Source Shortest Path):
# Find minimum time for node k signal to reach all nodes in
# a directed weighted graph
# Unlike Dijkstra:
# - Works even if graph contains negative weights
# - Does NOT rely on greedy heap expansion
# Core Idea:
# Repeatedly relax ALL edges
# Each full iteration allows shortest paths using
# one more edge to propagate through the graph
# After (V - 1) passes:
# shortest paths must be finalized
# (because longest simple path uses at most V-1 edges)
# Initialize distances:
# Distance array:
# dist[node] = shortest known time from k -> node
INF = float('inf')
# Nodes are 1-indexes, so size n+1
# sc: O(V)
dist = [INF] * (n + 1)
# Source node distance = 0
dist[k] = 0
# Relax Edges (V - 1) Times
# Relaxation:
# If going through improves distance to v, update it.
# Why V-1 loops?
# A shortest path can contain at most V-1 edges
# tc: O(V * E)
for i in range(n - 1):
# Optimization:
# If no update occurs during a pass,
# algorithm can stop early.
updated = False
# Process every edge
# tc per pass: O(E)
for u, v, w in times:
# Only relax if source node reachable
if dist[u] != INF and dist[u] + w < dist[v]:
# Relax edge (u -> v)
dist[v] = dist[u] + w
updated = True
# Early stopping condition:
# shortest paths already finalized
if not updated:
break
# Final Validation:
# Network delay = maximum shortests distance
# If nay node remains INF: unreachable
# tc: O(V)
max_dist = max(dist[1:])
# Return -1 if graph disconnected
if max_dist == INF:
return -1
# tc: O(V * E)
# sc: O(V)
return max_dist1631. Path With Minimum Effort ::1:: - Medium
Topics: Array, Binary Search, Depth First Search, Breadth First Search, Union Find, Heap (Priority Queue), Matrix
Intro
You are a hiker preparing for an upcoming hike. You are given heights, a 2D array of size rows x columns, where heights[row][col] represents the height of cell (row, col). You are situated in the top-left cell, (0, 0), and you hope to travel to the bottom-right cell, (rows-1, columns-1) (i.e., 0-indexed). You can move up, down, left, or right, and you wish to find a route that requires the minimum effort. A route's effort is the maximum absolute difference in heights between two consecutive cells of the route. Return the minimum effort required to travel from the top- left cell to the bottom-right cell.
| Example Input | Output |
|---|---|
| heights = [[1,2,2],[3,8,2],[5,3,5]] | 2 |
| heights = [[1,2,3],[3,8,4],[5,3,5]] | 1 |
Constraints:
rows == heights.length
columns == heights[i].length
1 ≤ rows, columns ≤ 100
1 ≤ heights[i][j] ≤ 106
Abstraction
Given a graph, determine the route with minimal climbing.
Space & Time Complexity
| Solution | Time Complexity | Space Complexity | Time Remark | Space Remark |
|---|---|---|---|---|
| Bug | Error |
|---|---|
Brute Force:
| Aspect | Time Complexity | Space Complexity | Time Remarks | Space Remarks |
|---|---|---|---|---|
Find the Bug:
Solution 1: Dijkstra + MinHeap - Advanced Graphs/Advanced Graphs
def minimumEffortPath(self, heights: List[List[int]]) -> int:
# Why Dijkstras + MinHeap?
# Dijkstras finds shortest path from a source node to all other nodes
# in a weighted graph with non-negative edge weights, our case
# Cell -> Node
# Effort (absolute height difference) -> Weight
# MinHeap ensures we always explore next cell with minimal effort first
# Guarantees the minimum maximum effort path to the bottom-right cell.
# Note:
# 1. Use MinHeap to track cells by minimal effort seen so far
# 2. Effort to reach a cell -> max(absolute difference along path)
# 3. Track visited/effort for each cell
# 4. Pop cell with lowest effort from heap, update neighbors
# 5. Stop when reaching bottom-right cell
# Result -> path of lowest effort
rows, cols = len(heights), len(heights[0])
efforts = [[float('inf')] * cols for _ in range(rows)]
efforts[0][0] = 0
# (effort, row, col)
min_heap = [(0, 0, 0)]
directions = [(0,1),(1,0),(-1,0),(0,-1)]
while min_heap:
curr_effort, r, c = heappop(min_heap)
# Reached target -> bottom right
if r == rows - 1 and c == cols - 1:
return curr_effort
for dr, dc in directions:
nr, nc = r + dr, c + dc
if 0 <= nr < rows and 0 <= nc < cols:
next_effort = max(curr_effort, abs(heights[r][c] - heights[nr][nc]))
if next_effort < efforts[nr][nc]:
efforts[nr][nc] = next_effort
heappush(min_heap, (next_effort, nr, nc))
# default, though problem guarantees a path exists
# overall: time complexity O(R*C*log(R*C)) due to heap operations
# overall: space complexity O(R*C) for effort tracking and heap
return 0778. Swim in Rising Water ::1:: - Hard
Topics: Array, Binary Search, Depth First Search, Breadth First Search, Union Find, Heap (Priority Queue), Matrix
Intro
You are given an n x n integer matrix grid where each value grid[i][j] represents the elevation at that point (i, j). It starts raining, and water gradually rises over time. At time t, the water level is t, meaning any cell with elevation less than equal to t is submerged or reachable. You can swim from a square to another 4-directionally adjacent square if and only if the elevation of both squares individually are at most t. You can swim infinite distances in zero time. Of course, you must stay within the boundaries of the grid during your swim. Return the minimum time until you can reach the
bottom right square (n - 1, n - 1) if you start at the top left square (0, 0).
| Example Input | Output |
|---|---|
| grid = [[0,2],[1,3]] | 3 |
| grid = [[0,1,2,3,4],[24,23,22,21,5],[12,13,14,15,16],[11,17,18,19,20],[10,9,8,7,6]] | 16 |
Constraints:
n == grid.length
n == grid[i].length
1 ≤ n ≤ 50
0 ≤ grid[i][j] < n2
Each value grid[i][j] is unique.
Abstraction
Given a graph, determine the time needed to traverse from top left to bottom right.
Space & Time Complexity
| Solution | Time Complexity | Space Complexity | Time Remark | Space Remark |
|---|---|---|---|---|
| Bug | Error |
|---|---|
Brute Force:
| Aspect | Time Complexity | Space Complexity | Time Remarks | Space Remarks |
|---|---|---|---|---|
Find the Bug:
Solution 1: Dijkstra + MinHeap - Advanced Graphs/Advanced Graphs
def swimInWater(self, grid: List[List[int]]) -> int:
# Why Dijkstras + MinHeap?
# Cell -> Node
# Weight -> determined by max elevation along path so far
# Dijkstras algo finds path from source (0,0) to target (n-1,n-1)
# that minimizes the max elevation
# MinHeap ensures we always expand the path with lowest current
# maximum elevation
# Guarantees minimum time t
# Result -> path of minimum height
# Note:
# 1. We want min time t to reach (n-1, n-1)
# 2. At any step, t = max elevation along the path
# 3. Use min-heap to always expand the path with lowest t so far
# 4. Track visited cells to avoid revisiting
n = len(grid)
visited = [[False] * n for _ in range(n)]
# (time_so_far, row, col)
min_heap = [(grid[0][0], 0, 0)]
directions = [(0,1),(1,0),(-1,0),(0,-1)]
while min_heap:
t, r, c = heappop(min_heap)
if visited[r][c]:
continue
visited[r][c] = True
# Reached target cell
if r == n - 1 and c == n - 1:
return t
for dr, dc in directions:
nr, nc = r + dr, c + dc
if 0 <= nr < n and 0 <= nc < n and not visited[nr][nc]:
# time to reach neighbor = max(current path t, neighbor elevation)
heappush(min_heap, (max(t, grid[nr][nc]), nr, nc))
# default, problem guarantees a path exists
# overall: time complexity O(n^2 * log(n^2)) due to heap operations
# overall: space complexity O(n^2) for heap and visited
return 0787. Cheapest Flights Within K Stops ::1:: - Medium
Topics: Dynamic Programming, Depth First Search, Breadth First Search, Graph, Heap (Priority Queue), Shortest Path
Intro
There are n cities connected by some number of
flights. You are given an array flights where flights[i] = [fromi, toi, pricei] indicates that pricei. You are also given three integers src, dst, and k, return the cheapest price from src to dst with at most k stops. If there is no such route, return -1.
| Example Input | Output |
|---|---|
| n = 4, flights = [[0,1,100],[1,2,100],[2,0,100],[1,3,600],[2,3,200]], src = 0, dst = 3, k = 1 | 700 |
| n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 1 | 200 |
Constraints:
1 ≤ n ≤ 100
0 ≤ flights.length ≤ (n * (n-1) / 2)
flight[i].length == 3
0 ≤ fromi, toi < n
fromi != toi
1 ≤ pricei ≤ 104
There will not be any multiple flights between two cities.
0 ≤ src, dst, k < n
src != dst
Abstraction
Given flights, determine the cheapest flights under k stops.
Space & Time Complexity
| Solution | Time Complexity | Space Complexity | Time Remark | Space Remark |
|---|---|---|---|---|
| Bug | Error |
|---|---|
Brute Force:
| Aspect | Time Complexity | Space Complexity | Time Remarks | Space Remarks |
|---|---|---|---|---|
Find the Bug:
Solution 1: Modified Dijkstra via BFS + MinHeap - Advanced Graphs/Advanced Graphs
def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, k: int) -> int:
# Modified Disjkstras?
# Modified for graphs with 'stops' constraint
# Each node in heap is (stops_so_far, current_node, cost_so_far)
# MinHeap guarantees we expand path with lowest cost so far
# Only continue paths that respect the stops limit (<= k)
# Build adjacency list
adj={i:[] for i in range(n)}
for u,v,w in flights:
adj[u].append((v,w))
# Initialize distance array and min-heap
dist=[float('inf')]*n
dist[src]=0
q=[]
# (stops_so_far, current_node, cost_so_far)
heapq.heappush(q,(0, src, 0))
# Process heap
while q:
stops,node,wei=heapq.heappop(q)
# Skip if stops exceed limit
if stops>k:
continue
# Explore neighbors
for nei,w in adj[node]:
next_cost = cost + w
# Only push if we improve distance
if dist[nei]>next_cost and stops<=k:
dist[nei]=next_cost
heapq.heappush(q,((stops+1,nei,next_cost)))
print(dist)
# Check if destination reachable
if dist[dst]==float('inf'):
return -1
res = dist[dst]
# overall: time complexity O(E log N) in practice, E = # of edges
# overall: space complexity O(N + E) for adjacency list and heap
return res